As many of you will know, electrons are not like planets orbiting their respective nucleus – the Rutherford-Bohr model was proven to be incorrect in the 1920s by Schrödinger and Heisenberg – but are rather act like a cloud. To be able to understand the atomic model, we must first look at the Uncertainty principle. In short, the exact position and momentum of an electron can never be known with absolute certainty – the more precisely you measure its momentum you are unable to know its position as accurately. So, electrons around an atom are modelled like a cloud of probability – worked out by the Schrödinger equation aka an electrons wavefunction.

The equation itself is quite confusing but I recently read a very good analogy (Quantum – Jim Al-Khalili) of the wave function. The police want to track a criminal who has recently burgled Southfields. They do not know where he is, but there is a high probability he will be in the surrounding buildings – time hasn’t passed much, and he is likely to go to the nearest building. But as time passes, he is less likely to be in nearby buildings and may have ventured farther out into Stamford, and it can be said that he’d be more likely to steal from the more expensive parts of town – more likely going to rob M&S than Savers. So as time passes, we do not know where the criminal is but we know areas that he is more likely to be. If he were to be spotted on a CCTV camera, we know for certain where he is – but for an extremely short time – and then the wave builds up again. That is the same for an electron.

In short, we never know the exact position and momentum of an electron, so we model it as areas of possibilities that spread out like a wave. Therefore, the modern model of an atom shows electrons orbiting in clouds around the nucleus. We never know exactly where they are, and they can have varying energies. When we observe an electron, its wavefunction collapses. The same principle can be applied to all extremely small things – electrons, protons, helium nuclei. Using this knowledge of electrons are able to be in multiple positions rather than a defined orbital path, we can look at photon emission.

Photon Emission:

Now, not only are the exact positions of electrons not every fully known, they can also have different energy states. Due to the nature of quantum theory, electrons can exist in discrete energy levels – n=1 being their ground state. In short, an electron can be excited if it receives the exact difference in energy between the ground state and the next energy level from an incoming photon. If they happen, the electron is excited and jumps energy levels. This is not a stable state to be in, and the electron wants to de-excite and return to its ground state. It does this by emitting a photon of the exact energy difference between levels, and this due to E=hf, means a photon of an exact frequency. That is the A-level understanding.

But that is known as spontaneous emission – we do not know when the electron is going to jump back down. However, passing a photon of the same energy difference (and frequency) as the energy gap between levels past the excited electron stimulates the emission of a photon from the electron. Further to this, the stimulated photon will be coherent (same frequency, wavelength, altitude, polarity, direction) to the one which stimulated it. How this works, is that an excited electron is hit again with a photon. Instead of making it move to a higher unstable energy level, the electron jumps back down giving out a coherent photon as well as the incident photon.

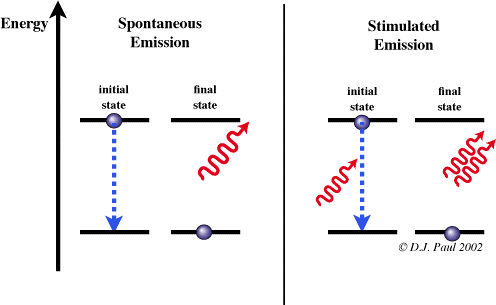
The Laser:

Now, we know about energy levels and electrons we can look at how lasers work. Laser stands for Light Amplification by Stimulated Emission of Radiation and using what we know about stimulated emission we can see how they work.

A laser is made of a gain medium – in which usually gaseous atoms (with electrons) are found – bookended by two mirrors. Surrounding the gain medium is the flash tube – an electric filed which is used to excite electrons. When a laser is given power, the flash tube releases photons which then excite the electrons of the atoms in the gain medium, getting them ready to emit photons. After some time, some of the electrons spontaneously jump back to ground state giving out photons. These photons pass by other atoms with excited electrons, which causes them to emit photons by stimulated emission. The flash tube keeps exciting the atoms, and as the photons reflect of the mirrors, we keep getting more and more coherent photons produced – all the exact same wavelength (well not the exact same wavelength, but extremely similar). After some time, the whole gain medium is swarming with photons, and all we need to do is open a small aperture in one of the mirrors and the photons are allowed to escape.

This is how most low powered lasers are made, but to be able to get extremely powerful research lasers we need to amplify the signal more so, and we don’t want to damage the equipment. This is where the most recent Nobel prize in physics comes from.

Chirped Pulse Amplification:

So, lasers are extremely useful for scientific research – like how stars work. But in order to do this we need lasers that provide high amounts of energy in a short space of time. If we simply kept increasing the intensity of the signal, we would break the laser trying to fire it. So we needed a way around this in order to get to a Petawatt of energy.

This is what ½ of the Nobel Prize for Physics was awarded last year. We want to stretch the pulse to decrease its intensity per second – its energy density. This allows us to amplify it up to the limit of the machine without breaking anything. But the trick is when we compress it back to its original size, it has a higher energy density than was possible from the base machine – allowing extremely high energy densities.

We are able to stretch the pulse as although the laser has wavelengths that are essentially the same – there are slight variations (due to some very complicated physics). Firing the pulse along a reflecting diffraction grating allows us to spread out the signal, and as the longer wavelength travels a shorter distance in the setup than the shorter wavelength. Red is shown to be the longer wavelength in the diagrams. This process is then reversed to compress the pulse, back into one extremely powerful signal.